Nếu bạn sống ở phía xa của Mặt trăng, làm thế nào bạn có thể suy ra sự tồn tại của Trái đất?

Giả sử rằng bạn ký gửi một nhà thiên văn học, được trang bị kiến ​​thức hiện tại của chúng ta về cơ học quỹ đạo, trên một mái vòm ở phía xa của Mặt trăng, để Trái đất được ẩn giấu vĩnh viễn khỏi chúng.

(Và, tất nhiên, giả sử rằng người này không có kiến ​​thức cụ thể về hệ thống mà họ vượt ra ngoài những gì họ có thể lượm lặt được từ các quan sát. Nếu bạn sẽ tưởng tượng rằng họ đã học tất cả các cơ học quỹ đạo hiện đại của chúng ta và vật lý liên quan trong alpha centauri, và sau đó được dịch chuyển đến Mặt trăng của chúng ta.)

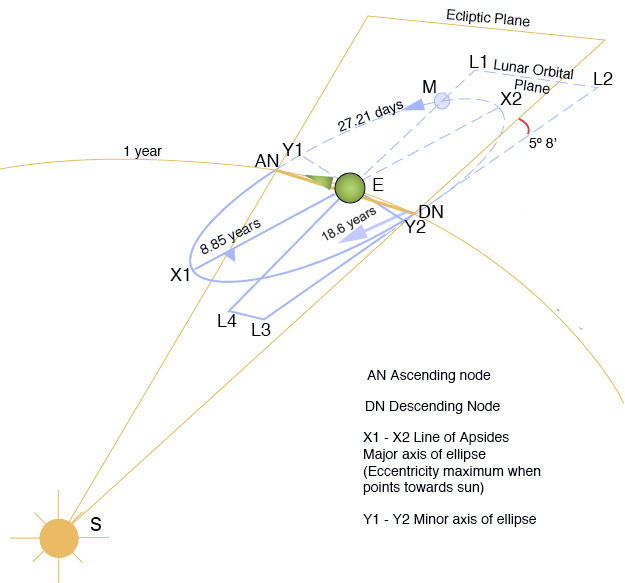
Bây giờ, thật hợp lý khi hy vọng rằng người này sẽ có thể suy ra từ các quan sát bầu trời mà cơ thể họ đang ở là một nửa của hệ thống nhị phân và họ có thể đo được các đặc điểm quỹ đạo (trục bán chính, tính elip, độ nghiêng) cũng như vị trí của barycentre (gần với cơ thể khác hơn, tương ứng với một đối tác lớn hơn nhiều). Những quan sát nào là cần thiết để suy luận điều này? Mức độ chính xác quan sát nào là cần thiết cho những quan sát đó, và nó tương ứng với thời đại lịch sử nào? (Tức là bộ của Tycho Brahe đã đủ chưa? Galileo? Người Hy Lạp cổ đại? Hay điều này sẽ đòi hỏi một đài quan sát cuối thế kỷ 19 (hoặc thậm chí muộn hơn)?)

(Như đã chỉ ra trong câu trả lời của MartinV, nhà thiên văn học của chúng ta có thể khó phân biệt giữa các tình huống với một cặp quỹ đạo với một cơ thể khổng lồ duy nhất. Vì vậy, nếu thuận tiện, bạn có thể giả sử rằng, thông qua các khoảng cách ngắn 100km từ mái vòm, nhà thiên văn học của chúng ta có thể đo bán kính mặt trăng bằng cách đo độ nghiêng của mặt trời tại các điểm khác nhau với khoảng cách đã biết giữa chúng, à la Erathostenes .)

Một máy đo địa chấn thủy triều cơ thể ở phía xa mặt trăng sẽ đón cả thủy triều mặt trời và biến dạng cơ thể 20 inch do trái đất tạo ra . Trong khi "khóa chặt", mặt trăng không nằm trong quỹ đạo tròn hoàn hảo, và cũng chao đảo một chút; hiệu chuẩn . Máy đo địa chấn của bạn nên nhận cả hai hiệu ứng.

Theo dõi thị sai của chu kỳ sao hỏa cứ sau 28 ngày, như được đề xuất trong các bình luận ở trên, có thể là một cách đơn giản hơn để đi.

Đây là một câu hỏi thực sự tốt - và khá tinh tế.

TL; DR;

Cơ hội sớm nhất có thể là sự thay đổi giữa các tháng trong thị sai của Mặt trời có thể khiến người quan sát kết luận rằng tôi) Mặt trăng là một vật thể đơn, rất lớn, xoay tròn hoặc ii) nó là một phần của một cơ thể đa thể hệ thống quay. Tuy nhiên i) dường như không phù hợp với đường chân trời cong và gần.

Nếu không thì chắc chắn khi chúng ta phát triển một mô hình định lượng của cơ học quỹ đạo liên quan đến khối lượng và trọng lực

Tôi không nghĩ thị sai sao sẽ trực tiếp giúp chúng ta vì nó (trong thời hiện đại) chỉ cho chúng ta biết rằng chúng ta đang ở trên quỹ đạo quanh mặt trời và rất ít về chính hệ Mặt trăng Trái đất.

Chúng ta hãy xem làm thế nào một Ptolemy tương đương trên Mặt trăng (gọi anh ta là Moon-Ptolemy) có thể thấy nó. Anh ta sẽ không có cách nào phân biệt hệ Mặt trăng Trái đất với giả định rằng anh ta chỉ ngồi trên một vật thể rắn ở trung tâm của sự sáng tạo. Tất nhiên anh ta sẽ không nhìn thấy một "mặt trăng" trên quỹ đạo xung quanh mình, nhưng anh ta sẽ nhìn thấy Mặt trời, các ngôi sao và các hành tinh lớn. Thị sai của sao (đối với anh ta, Mặt trời "di chuyển qua cung hoàng đạo) sẽ chỉ cho anh ta biết rằng Mặt trời đang quay quanh Mặt trăng của anh ta, cũng như các hành tinh. Sự tồn tại của các vòng quay hành tinh sẽ là một sự tò mò cần thiết để làm cho mô hình của anh ta hoạt động - nhưng nó thực sự làm việc và anh ta không có khái niệm về Trái đất

Moon-Galileo có thể (hoặc có thể không) có thể phát triển mô hình nhật tâm - anh ta bỏ lỡ một cái nhìn sâu sắc quan trọng mà Trái đất-Galileo có: Trái đất không đặc biệt vì các hành tinh khác cũng có mặt trăng. Moon-Galileo sẽ thấy hệ thống quỹ đạo của Sao Mộc thú vị nhưng không phải là một cái nhìn sâu sắc quan trọng, vì vậy ông có thể không phát triển mô hình mới. Mặc dù vậy, một người khác sẽ.

Tuy nhiên, trong một thế giới khoa học định tính, vẫn sẽ không có gì giúp người quan sát Mặt trăng suy luận sự tồn tại của Trái đất đằng sau đường chân trời.

Tôi nghi ngờ sự thật sẽ trở nên không thể tránh khỏi khi cơ học quỹ đạo phát triển đủ để kết hợp khối lượng và trọng lực vào tính toán. Nó có thể là khoảng thời gian của Moon-Kepler.

Tôi không chắc chắn tôi đồng ý với các nhận xét khi quan sát các hành tinh - Tôi không thấy cách chúng giúp phân biệt giữa hệ Mặt trăng Trái đất trái ngược với cơ thể Mặt trăng quay đơn giản, rất lớn, không có quỹ đạo ( đó sẽ là một giả định tự nhiên để thực hiện). Ngay cả những thay đổi hàng tháng về thị sai gây ra bởi sự quay của Mặt trăng quanh Trái đất cũng có thể bị xóa đi bằng cách gợi ý sự quay đơn giản của một cơ thể Mặt trăng lớn hơn nhiều - mặc dù anh hùng của chúng ta chắc chắn có thể nghi ngờ sự tương thích của điều này với độ cong và khoảng cách rõ ràng với chúng Chân trời trăng.

Một người quan sát ở phía xa của mặt trăng sẽ khó có thể giải thích nó đứng trên một hành tinh duy nhất, bởi vì sự chuyển động của thứ đáng chú ý nhất trên bầu trời: mặt trời!

Thật vậy, do độ lệch tâm của quỹ đạo của mặt trăng quanh trái đất, độ dài ngày, tức là "tốc độ trên bầu trời" của mặt trời, phụ thuộc vào vị trí bạn đứng trong quỹ đạo mặt trăng của bạn.

Và từ những quan sát có thể làm, ví dụ, các hành tinh khác có hình tròn gần như hoàn hảo trong hệ mặt trời (và vì những lý do nổi tiếng), cô nên bị buộc phải loại trừ giả thuyết "Tôi đang đứng trên một thiên thể đơn hình elip".

Tôi không thể tính được sự thay đổi của độ dài ngày ở phía xa của mặt trăng trong một khoảng thời gian hợp lý, xin lỗi về điều đó.

Một hiệu ứng khác mà tôi sẽ cố gắng minh họa bằng các hình ảnh Wikipedia: độ cao của quỹ đạo mặt trời trên bầu trời sẽ thay đổi theo từng năm (chu kỳ: từ 8 đến 9 năm trái đất), do sự suy thoái của mặt trăng và kế hoạch quỹ đạo nghiêng của nó:

Bởi Rfassbind - Công việc riêng., Miền công cộng, Liên kết

Theo nhà địa chất, Homunculus 2 - từ Wikipedia tiếng Anh, CC BY 3.0 , Link