Bạn đã bỏ lỡ yếu tố quan trọng nhất, đó là, mặt trời ở gần như thế nào và là kết quả của khoảng cách với mặt trời và khối lượng tương đối, quả cầu Hill và khoảng cách gần đúng khi khoảng cách quỹ đạo ổn định kết thúc .
Động lượng góc để đánh giá mặt trăng bị đẩy ra khỏi hành tinh là sự kết hợp thú vị của các công thức và có thể được tính dựa trên các yếu tố bạn đã đề cập, mật độ, khối lượng, kích thước, hình dạng và khối lượng của các đại dương lỏng trên bề mặt, tỷ lệ xoay, v.v ... Có lẽ không phải là một phép tính gần đúng phức tạp có thể được xử lý cho các kịch bản khác nhau để cho thấy một mặt trăng sẽ di chuyển bao xa trước khi hệ thống khóa chặt và mất bao lâu. (một số hệ thống tương tác ít hơn có thể mất hàng nghìn tỷ hoặc bốn triệu năm hoặc lâu hơn để đạt đến vị trí tương đối cuối cùng, so với khoảng 50 tỷ hoặc hơn thời gian biểu để hệ thống Mặt trăng Trái đất khóa chặt.
Nhưng nếu chúng ta xem Mặt trăng-Trái đất-Mặt trăng là một ví dụ, thì điều quan trọng nhất về việc Trái đất có mất mặt trăng hay không là phần phần ổn định của Sphere Hill kéo dài bao xa, nếu khối lượng của cả 3 vật thể là như thế nào bây giờ, yếu tố chính là Trái đất ở gần Mặt trời như thế nào. Nếu Trái đất ở gần Mặt trời như Sao Kim, Mặt trăng có thể sẽ thoát ra, nhưng sẽ mất một thời gian. Nếu Trái đất gần mặt trời như sao Thủy (trung bình), nó sẽ mất Mặt trăng từ lâu.
OK, tôi nghĩ rằng tôi có một lối vào đơn giản cho các câu hỏi khác của bạn, ít nhất là một nơi tốt để bắt đầu. Động lượng góc.
Nếu chúng ta xem xét một hệ thống quỹ đạo hai cơ thể thì hiệu ứng thủy triều trên quỹ đạo là khá thẳng về phía trước. Xem xét các hệ thống nơi phình xoay trước mặt trăng, mặt trăng đang dần dần bị đẩy ra khỏi hành tinh và vòng quay của hành tinh giảm dần.
Trong hệ thống hai cơ thể này, mặt trăng không bao giờ thoát ra vì trong một hệ thống hai cơ thể, quỹ đạo vẫn ổn định trong một khoảng cách rất lớn, về cơ bản câu hỏi sẽ trở thành, mặt trăng di chuyển bao xa và mất bao lâu cho đến khi hệ thống bị khóa chặt ở đâu , ít nhất là về mặt toán học, đạt đến trạng thái kết thúc.
Cơ thể thứ 3 trong ảnh (Mặt trời) có hiệu ứng theo một vài cách. Mối quan hệ giữa khối lượng và khoảng cách tương đối của Mặt trời và Hành tinh xác định ranh giới gần đúng của vùng ổn định của Sphere Hill, ngoài đó mặt trăng có khả năng thoát ra. Mặt trời cũng kéo theo Mặt trăng, tạo ra nhiễu loạn trên quỹ đạo của nó và làm cho nó không cong, trong khi đó, so sánh, hai hệ thống cơ thể với mặt trăng bị đẩy ra xa chuyển sang hình tròn.
Đối với các sao lùn đỏ, nơi các hành tinh ở gần ngôi sao, hành tinh bị khóa chặt với ngôi sao lùn đỏ sẽ trở nên nhiều khả năng hơn (mặc dù một số trường hợp bị khóa một phần như tỷ lệ quay 3/2 của sao Thủy có thể xảy ra) các trường hợp, với một ngôi sao lùn đỏ và các hành tinh tương đối gần nhau, hành tinh này bị khóa chặt với ngôi sao và quay chậm hơn so với mặt trăng, dẫn đến quỹ đạo phân rã của các mặt trăng đối với các hành tinh của chúng trong các hệ sao lùn đỏ. Vùng quỹ đạo ổn định trong các hệ thống như vậy cũng sẽ nhỏ hơn nhiều. Mặt trời là một yếu tố quan trọng trong chuyển động của mặt trăng đến hoặc từ các hành tinh.
Nhưng quay trở lại hệ thống 2 cơ thể và ước tính hiệu ứng thủy triều, biết rằng mặt trăng sẽ không bao giờ thoát khỏi hệ thống hai cơ thể kín, câu hỏi đặt ra là Mặt trăng có thể di chuyển từ hành tinh bao xa và mất bao lâu cho đến khi khóa thủy triều lẫn nhau là đạt được.
Mặt trăng có thể đi được bao xa từ hành tinh có thể được ước tính bằng tổng động lượng góc của hệ, vì vậy bạn chính xác rằng tốc độ quay ban đầu là một yếu tố, khối lượng tương đối giữa Hành tinh và Mặt trăng cũng vậy. Một mặt trăng lớn hơn tạo ra một khối thủy triều lớn hơn trên hành tinh, kết quả là Mặt trăng di chuyển ra khỏi hành tinh nhanh hơn một mặt trăng nhỏ hơn. Đồng thời, mặt trăng lớn hơn đòi hỏi động lượng góc hơn khi nó di chuyển ra khỏi hành tinh, do đó nó di chuyển ít hơn. Một mặt trăng nhỏ hơn di chuyển xa hơn nhưng mất nhiều thời gian hơn để đến đó và khóa thủy triều cũng mất nhiều thời gian hơn để xảy ra.
Một hành tinh lỏng hơn sẽ trải qua thủy triều mạnh hơn, một lần nữa sẽ làm nó chậm lại nhanh hơn, nhưng chắc chắn sẽ tăng tốc vệ tinh nhanh hơn. Một chất lỏng nhớt hơn nước sẽ trải qua thủy triều yếu hơn, nhưng tôi nghĩ rằng chúng sẽ ở phía trước xa hơn. Tôi nghĩ rằng nhiều chất lỏng chắc chắn là hiệu quả hơn, nhưng có vẻ ít rõ ràng hơn điểm đầu tiên.
Thật không đúng khi nói một hành tinh lỏng hơn sẽ trải qua những đợt thủy triều mạnh hơn. Nói rằng nó sẽ trải qua thủy triều cao hơn so với nếu nó rắn sẽ chính xác hơn. Thủy triều trải nghiệm hành tinh phụ thuộc vào khối lượng và khoảng cách của Mặt trăng và kích thước của hành tinh, do đó Mặt trăng bằng nhau, thủy triều sẽ giống nhau cho dù hành tinh này ở dạng lỏng hay rắn. Chất lỏng ít cứng hơn, vì vậy chúng tốt hơn trong việc tạo ra thủy triều, nhưng cũng có thủy triều trên đất liền. Trên Trái đất, chúng được gọi là thủy triều .
Thủy triều cao hơn thực sự đẩy Mặt trăng tốt hơn và làm chậm hành tinh nhanh hơn và chất lỏng phản ứng với thủy triều hiệu quả hơn, do đó, các hành tinh có bề mặt chất lỏng di chuyển các mặt trăng của chúng hiệu quả hơn và nhanh hơn các hành tinh không có bề mặt chất lỏng. Hình dạng của các đại dương cũng vậy. Thái Bình Dương rộng hơn có thủy triều lớn hơn Đại Tây Dương hẹp hơn.
Nguồn
Tôi không tin độ nhớt của chất lỏng. Chất lỏng chảy, chất rắn không và cha đi trước cũng không đúng. Các hành tinh thường quay như một đơn vị, mặc dù có sự khác biệt nhỏ giữa tốc độ quay giữa lõi và lớp phủ, toàn bộ hành tinh quay và phình thủy triều quay cùng với nó. Chất lỏng hiệu quả hơn và phình ra, nhưng không phải là cách mà khối phồng di chuyển về phía trước với vòng quay của hành tinh ở các góc bằng nhau trước mặt trăng.
Một hành tinh lớn hơn sẽ có quỹ đạo bị chậm lại do gia tốc thủy triều, nhưng có lực kéo mạnh hơn để thoát ra. Một vệ tinh lớn hơn sẽ gây ra thủy triều mạnh hơn và lực thủy triều mạnh hơn, nhưng sẽ cần nhiều lực hơn để tăng tốc, và sẽ làm hành tinh chậm lại nhanh hơn. Tôi thực sự không thể biết cái nào có tác dụng mạnh hơn ...
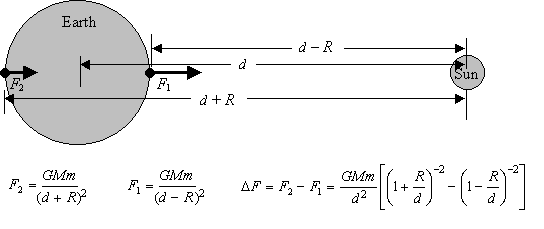
Ở đây bạn phải cẩn thận vì nó phức tạp hơn một chút. Lực thủy triều mà một hành tinh trải nghiệm từ mặt trăng của nó phải liên quan đến khối lượng của mặt trăng, khoảng cách của mặt trăng, nhưng cũng là khối lượng của hành tinh và bán kính của hành tinh.
Nhìn vào những con số:
Nguồn
phần thứ hai của công thức khá phức tạp,[(1+R/d)−2−(1−R/d)−2]
nhưng nếu bạn tính toán toán cho các mặt trăng khá xa, sự khác biệt về lực thủy triều từ phía xa của hành tinh đến phía gần là về:
ΔF=−4GMmRd3
Vì vậy, nhìn vào hệ thống Trái đất-Mặt trăng, bỏ qua mặt trời bây giờ.
Nếu bạn tạo ra Trái đất có cùng kích thước nhưng khối lượng gấp đôi, lực thủy triều tăng gấp đôi nhưng trọng lực bề mặt của Trái đất sẽ tăng gấp đôi, sẽ khiến nước biển có trọng lượng gấp đôi với khối lượng bằng nhau, lực trên Mặt trăng sẽ tương tự, nhưng Trái đất nặng hơn sẽ mất nhiều thời gian hơn để làm chậm, vì vậy hiệu quả là Mặt trăng sẽ di chuyển xa hơn, không xa hơn.
Nếu bạn giữ mật độ như nhau và làm cho Trái đất lớn hơn, hãy nói gấp 8 lần khối lượng, gấp đôi đường kính. Lực thủy triều mà Mặt trăng tác động lên siêu trái đất mới của chúng ta sẽ lớn gấp 16 lần nhưng lực hấp dẫn trên bề mặt Trái đất chỉ gấp đôi. Điều đó có nghĩa là bằng cách làm cho hành tinh lớn hơn, Mặt trăng thực sự di chuyển nhanh hơn. Hành tinh lớn hơn (nhưng mật độ bằng nhau) sẽ chậm lại với tốc độ gần bằng nhau nhưng khi Mặt trăng di chuyển đi thì tốc độ đó sẽ chậm lại.
Một số toán học về thủy triều gây nhầm lẫn cho tôi. Lực thủy triều nghịch đảo di chuyển các mặt trăng ra khỏi các hành tinh giảm đáng kể theo khoảng cách. Các lực thủy triều rơi xuống với khối lập phương từ xa. Lực từ phồng thủy triều có thể giảm xuống nhanh hơn thế bởi vì góc giảm theo khoảng cách, (tôi đoán nó giảm xuống bởi sức mạnh thứ 4), do đó, khi khoảng cách của Mặt trăng từ Trái đất tăng gấp đôi, tốc độ di chuyển của nó giảm xuống bằng (khoảng), 16 lần. (((Tôi nghĩ))).
Vì vậy, nếu bạn làm cho Trái đất lớn gấp 8 lần và bán kính gấp đôi, lực thủy triều tăng thêm 16, nhưng nếu Mặt trăng di chuyển xa gấp đôi, thì lực thủy triều giảm 16, đó là loại gọn gàng mà nó hủy bỏ. Khoảng cách với tỷ lệ trọng lực, giả sử Mặt trăng không thay đổi và mật độ của hành tinh không thay đổi, là 1 trên 1, đó là điều tôi mong đợi.
Điều đó có thể lâu hơn nó nên và nó có thể cần phải dọn dẹp nhiều, nhưng tôi cần gọi nó là một ngày, vì vậy tôi sẽ xem xét vào ngày mai.

