Vấn đề có thể được giải quyết trong O (polylog (b)).
Chúng tôi xác định f(d, n)là số nguyên có tối đa d chữ số thập phân với tổng chữ số nhỏ hơn hoặc bằng n. Có thể thấy rằng chức năng này được đưa ra bởi công thức

Hãy lấy chức năng này, bắt đầu với một cái gì đó đơn giản hơn.
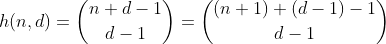
Hàm h đếm số cách để chọn các phần tử d - 1 từ một tập hợp đa chứa n + 1 phần tử khác nhau. Đây cũng là số cách để phân chia n thành các thùng d, có thể dễ dàng nhìn thấy bằng cách xây dựng hàng rào d - 1 xung quanh n hàng rào và tổng hợp từng phần riêng biệt. Ví dụ cho n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Vì vậy, h đếm tất cả các số có tổng chữ số gồm n và d chữ số. Ngoại trừ nó chỉ hoạt động cho n dưới 10, vì các chữ số được giới hạn ở 0 - 9. Để sửa lỗi này cho các giá trị 10 - 19, chúng ta cần trừ đi số lượng phân vùng có một thùng có số lớn hơn 9, từ bây giờ tôi sẽ gọi các thùng đầy tràn.
Thuật ngữ này có thể được tính bằng cách sử dụng lại h theo cách sau. Chúng tôi đếm số cách để phân vùng n - 10, sau đó chọn một trong các thùng để đặt 10 vào, điều này dẫn đến số lượng phân vùng có một thùng bị tràn. Kết quả là chức năng sơ bộ sau đây.
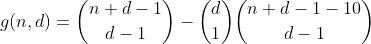
Chúng tôi tiếp tục theo cách này cho n ít hơn hoặc bằng 29, bằng cách đếm tất cả các cách phân vùng n - 20, sau đó chọn 2 thùng trong đó chúng tôi đặt 10 số vào đó, qua đó đếm số lượng phân vùng chứa 2 thùng tràn.
Nhưng tại thời điểm này, chúng tôi phải cẩn thận, bởi vì chúng tôi đã đếm các phân vùng có 2 thùng tràn trong nhiệm kỳ trước. Không chỉ vậy, nhưng thực sự chúng tôi đã đếm chúng hai lần. Chúng ta hãy sử dụng một ví dụ và xem xét phân vùng (10.0,11) với tổng số 21. Trong thuật ngữ trước, chúng tôi đã trừ 10, tính tất cả các phân vùng của 11 còn lại và đặt 10 vào một trong 3 thùng. Nhưng phân vùng cụ thể này có thể đạt được theo một trong hai cách:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Vì chúng tôi cũng đã đếm các phân vùng này một lần trong thuật ngữ đầu tiên, tổng số phân vùng có 2 thùng bị tràn lên tới 1 - 2 = -1, vì vậy chúng tôi cần đếm chúng một lần nữa bằng cách thêm thuật ngữ tiếp theo.
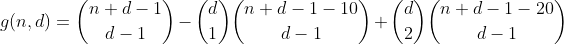
Nghĩ về điều này nhiều hơn một chút, chúng tôi sớm phát hiện ra rằng số lần phân vùng có số lượng thùng tràn cụ thể được tính trong một thuật ngữ cụ thể có thể được biểu thị bằng bảng sau (cột i đại diện cho thuật ngữ i, phân vùng j với j tràn thùng).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Vâng, đó là tam giác Pascals. Số lượng duy nhất chúng tôi quan tâm là một trong hàng / cột đầu tiên, tức là số lượng phân vùng với các thùng không tràn. Và vì tổng số xen kẽ của mỗi hàng nhưng đầu tiên bằng 0 (ví dụ 1 - 4 + 6 - 4 + 1 = 0), đó là cách chúng tôi loại bỏ chúng và đi đến công thức áp chót.
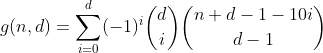
Hàm này đếm tất cả các số có d chữ số có tổng bằng n.
Bây giờ, những con số có tổng số nhỏ hơn n thì sao? Chúng ta có thể sử dụng một phép lặp lại tiêu chuẩn cho nhị thức cộng với một đối số quy nạp, để chỉ ra rằng
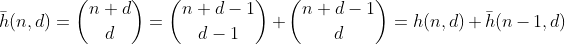
đếm số lượng phân vùng có tổng chữ số nhiều nhất là n. Và từ f này có thể được suy ra bằng cách sử dụng các đối số tương tự như đối với g.
Ví dụ, sử dụng công thức này, chúng ta có thể tìm thấy số lượng các số nặng trong khoảng từ 8000 đến 8999 vì 1000 - f(3, 20), beacuse có hàng ngàn số trong khoảng này và chúng ta phải trừ đi số lượng các số có tổng chữ số nhỏ hơn hoặc bằng 28 trong khi tham gia để chứng minh rằng chữ số đầu tiên đã đóng góp 8 vào tổng chữ số.
Như một ví dụ phức tạp hơn, hãy nhìn vào số lượng các số nặng trong khoảng 1234..5678. Trước tiên chúng ta có thể đi từ 1234 đến 1240 theo các bước 1. Sau đó, chúng ta đi từ 1240 đến 1300 ở các bước 10. Công thức trên cho chúng ta số lượng số nặng trong mỗi khoảng như vậy:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Bây giờ chúng tôi đi từ 1300 đến 2000 theo các bước 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
Từ 2000 đến 5000 trong các bước 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Bây giờ chúng ta phải giảm kích thước bước một lần nữa, từ 5000 xuống 5600 ở các bước 100, từ 5600 xuống 5670 ở các bước 10 và cuối cùng từ 5670 xuống 5678 ở các bước 1.
Một ví dụ về triển khai Python (đã nhận được tối ưu hóa và thử nghiệm trong khi đó):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Chỉnh sửa : Thay thế mã bằng một phiên bản được tối ưu hóa (trông thậm chí còn xấu hơn mã gốc). Cũng sửa một vài trường hợp góc trong khi tôi đang ở đó. heavy(1234, 100000000)mất khoảng một phần nghìn giây trên máy của tôi.
