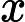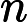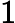Làm thế nào tôi có thể xác minh một giải pháp cho vấn đề nhân viên bán hàng du lịch trong thời gian đa thức?

31

Vì vậy, vấn đề quyết định TSP (vấn đề nhân viên bán hàng du lịch) là NP hoàn tất .

Nhưng tôi không hiểu làm thế nào tôi có thể xác minh rằng một giải pháp nhất định cho TSP trên thực tế là tối ưu trong thời gian đa thức, vì không có cách nào để tìm giải pháp tối ưu trong thời gian đa thức (đó là do vấn đề không nằm ở P)?

Bất cứ điều gì có thể giúp tôi thấy rằng việc xác minh trên thực tế có thể được thực hiện trong thời gian đa thức?

complexity-theory np-complete traveling-salesman

— Lazer
nguồn

20

Để được chính xác hơn, chúng tôi không biết nếu TSP là tại . Có thể là nó có thể được giải quyết trong thời gian đa thức, mặc dù có lẽ là niềm tin chung là . Bây giờ, hãy nhớ lại ý nghĩa của một vấn đề là -hard và -complete, xem ví dụ câu trả lời của tôi ở đây . Tôi tin rằng nguồn của bạn của sự nhầm lẫn bắt nguồn từ các định nghĩa: một -Hard vấn đề không nhất thiết phải ở . $\mathsf{P}$ $\mathsf{P} \neq \mathsf{NP}$ $\mathsf{NP}$ $\mathsf{NP}$ $\mathsf{NP}$ $\mathsf{NP}$

Khi bạn và trang Wikipedia bạn liên kết trạng thái, vấn đề quyết định là -complete: đưa ra chi phí và số nguyên , quyết định xem có chuyến tham quan nào rẻ hơn . Một cách để nhìn nhận vấn đề là trong là để thấy rằng đưa ra một giải pháp, thật dễ dàng để xác minh trong thời gian đa thức cho dù giải pháp đó rẻ hơn . Làm thế nào bạn có thể làm điều này? Chỉ cần theo dõi chuyến tham quan đã đưa ra, ghi lại tổng chi phí của nó và cuối cùng so sánh tổng chi phí với . $\mathsf{NP}$ $x$ $x$ $\mathsf{NP}$ $x$ $x$

— Juho
nguồn

"Chỉ cần theo dõi chuyến tham quan đã đưa ra, ghi lại tổng chi phí của nó và cuối cùng so sánh tổng chi phí với x." -> Có, nhưng có số lượng tour du lịch theo cấp số nhân để kiểm tra!

— Lazer

2

Tôi chỉ là một chút quá chậm, có vẻ như. ;-)

— Niel de Beaudrap

3

@Lazer Không, có chính xác một tour để kiểm tra. Bạn được đưa ra một tour du lịch và bạn ghi lại chiều dài của nó. Nếu nó nhỏ hơn

, đầu ra có , nếu không thì không .

x

$x$

— Juho

"quyết định xem có tour du lịch không" điều này chắc chắn có nghĩa là chúng tôi không được tham gia tour. Tôi đang thiếu gì?

— Lazer

3

@Lazer Không, trong vấn đề bạn được đưa ra một biểu đồ có trọng số và chi phí mục tiêu. Giấy chứng nhận là một tour du lịch. Đối với một lời giải thích khác, xem câu trả lời của Niel. Giống như trong ví dụ trên Wiki trong trường hợp SUBSET-SUM, chúng tôi không được cho số không, nhưng thay vào đó chúng tôi được cung cấp một tập hợp con cụ thể dưới dạng chứng chỉ.

— Juho

34

Mấu chốt là bạn phải xem xét vấn đề quyết định :

Vấn đề nhân viên bán hàng du lịch (Phiên bản quyết định). Cho một đồ thị có trọng số G và chi phí mục tiêu C , có chu trình Hamilton trong G có trọng lượng nhiều nhất là C không?

Đối với một 'có' dụ, giấy chứng nhận chỉ là một số chu trình Hamilton có trọng lượng tối đa là C . Nếu bạn có thể giải quyết vấn đề này một cách hiệu quả, bạn có thể tìm thấy chi phí của một chuyến tham quan tối thiểu bằng cách tìm kiếm nhị phân, bắt đầu với trọng số của toàn bộ mạng là giới hạn trên.

— Niel de Beaudrap
nguồn

3

Có lẽ bạn đang nghĩ về vấn đề xác định liệu một giải pháp nhất định cho TSP có phải là giải pháp tốt nhất hay không . Tuy nhiên, không có giải pháp đa thức nào được biết cho điều này, điều đó có nghĩa là vấn đề này nằm ở NP-hard, nhưng không nhất thiết là NP-Complete.

Vấn đề Quyết định TSP thực sự là về việc xác định xem trọng số của bất kỳ giải pháp nào trong đồ thị Gcó giá cao nhất C(như được giải thích tốt hơn trong câu trả lời của Niel), điều này chắc chắn có thể kiểm chứng được trong thời gian đa thức.

— Casey Kuball
nguồn

5

Xin lỗi cho nhà sư phạm, nhưng TSP không phải là NP-hard vì có các tour

. Ví dụ, sắp xếp là trong P mặc dù có

hoán vị có thể là tốt. Không gian tìm kiếm lớn hoặc nhanh chóng không bao giờ ngụ ý độ cứng.

O (n!)

$O(n!)$

n!

$n!$

— Juho

@Juho Có thể xác minh rằng một chuỗi được sắp xếp, bằng cách kiểm tra xem

. Tuy nhiên, để biết rằng một cái gì đó là giải pháp TỐT NHẤT cho TSP, cần phải biết rằng chi phí là chi phí tối thiểu, vốn dĩ đòi hỏi phải biết tất cả các chi phí khác.

n_{0} <= n_{1} <= . . .

$n_0 <= n_1 <= ...$

— Casey Kuball

4

Không, bạn có thể đạt được mức tối ưu ngay cả khi không tính toán độ dài của tất cả các chuyến tham quan khác. Và vâng, có thể chứng minh điều này thực tế là tối ưu mà không cần tính toán tất cả các tour du lịch khác. Đối với một ví dụ xem xét chi nhánh và ràng buộc.

— Juho

7

Tất cả những gì tôi nói là không gian tìm kiếm khổng lồ không nhất thiết có nghĩa là vấn đề khó khăn. Ngay cả khi chúng ta ví dụ không biết về một thuật toán tốt hơn so với brute-force liệt kê tất cả các khả năng, điều đó không có nghĩa đó là thuật toán duy nhất ngoài kia. Lập trình động là ví dụ điển hình ngay cả ở đây: thuật toán Held-Karp là thuật toán chính xác cho TSP chạy trong thời gian

. Xin lỗi, điều này được cho là chỉ gây nghiện, nhưng tôi chỉ muốn thêm một lời nhắc :)

O (n^{2} 2^{n})

$O(n^22^n)$

— Juho

@Juho điểm tốt. Tôi đã cập nhật câu trả lời để không còn chỉ ra lực lượng vũ phu là lựa chọn duy nhất (chỉ có điều là không có bất kỳ giải pháp đa thức nào).

— Casey Kuball

2

Bạn có thể chỉ ra rằng nó là tối ưu khi đưa ra một lời tiên tri giải quyết vấn đề quyết định (xem các câu trả lời khác) trong thời gian đa thức bằng cách truy vấn nếu có tồn tại một giải pháp ngắn hơn. Nếu mục tiêu của bạn là xây dựng một giải pháp tối ưu dựa trên lời tiên tri, hãy tiến hành như sau. Tìm tổng trọng lượng tối thiểu thông qua tìm kiếm nhị phân (hoặc nếu có trọng số cạnh không nguyên, hãy tìm tổng trọng số khác với mức tối thiểu nhỏ hơn chênh lệch tối thiểu giữa hai trọng số cạnh). Gọi giá trị này . Đối với mỗi cạnh trong đồ thị, loại bỏ cạnh, và truy vấn oracle để xem nếu vẫn còn là một giải pháp tối nhất . Nếu vậy, hãy để các cạnh ra, và tiếp tục. Nếu không, đặt cạnh lại và tiếp tục. Khi bạn đã xử lý tất cả các cạnh, bạn sẽ còn lại một chu kỳ Hamilton có trọng lượng tối thiểu. $M$ $M$

— Đệ quy
nguồn