Có thể tránh được các bước phân chia các bước trong một loại hợp nhất?

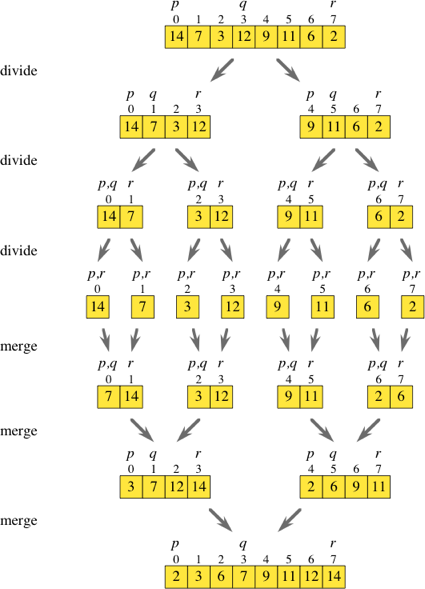
Hợp nhất sắp xếp

Vì vậy, hợp nhất sắp xếp là một thuật toán phân chia và chinh phục. Trong khi tôi đang nhìn vào sơ đồ trên, tôi đã suy nghĩ liệu về cơ bản có thể bỏ qua tất cả các bước phân chia hay không.

Nếu bạn lặp lại qua mảng ban đầu trong khi nhảy bằng hai, bạn có thể lấy các phần tử tại chỉ mục i và i + 1 và đặt chúng vào các mảng được sắp xếp riêng của chúng. Khi bạn có tất cả các mảng con này ([7,14], [3,12], [9,11] và [2,6] như trong sơ đồ), bạn chỉ cần thực hiện quy trình hợp nhất thông thường để có được một mảng được sắp xếp.

Việc lặp qua mảng và ngay lập tức tạo ra các mảng con cần thiết có hiệu quả thấp hơn so với việc thực hiện toàn bộ các bước phân chia?

— Jimmy_Rustle
nguồn

Liên quan: cs.stackexchange.com/questions/77075/ Kẻ

— Omar

Câu trả lời:

Sự nhầm lẫn xuất phát từ sự khác biệt giữa mô tả khái niệm của thuật toán và việc thực hiện nó .

Sắp xếp hợp lý hợp lý được mô tả là chia mảng thành các mảng nhỏ hơn, và sau đó hợp nhất chúng lại với nhau. Tuy nhiên, "tách mảng" không có nghĩa là "tạo ra một mảng hoàn toàn mới trong bộ nhớ", hoặc bất cứ điều gì tương tự - nó có thể được thực hiện theo mã như

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

tức là không có công việc thực tế diễn ra, và "chia tách" hoàn toàn là khái niệm. Vì vậy, những gì bạn đề xuất chắc chắn sẽ hoạt động, nhưng về mặt logic, bạn vẫn "chia tách" các mảng - bạn không cần bất kỳ công việc nào từ máy tính để làm như vậy :-)

— psmears
nguồn

Cá nhân tôi thực sự thích cách sắp xếp hợp nhất từ dưới lên vì thực hiện đơn giản hơn theo cách cho phép bạn tránh phân bổ bộ đệm tạm thời ở mỗi cấp độ đệ quy. Thay vào đó, bạn phân bổ bộ đệm một lần và bóng bàn giữa chúng.

— quái vật ratchet

Sự phân chia này được tính toán là không có ... cộng với gợi ý OP chỉ là phần giới thiệu tương đương với việc hợp nhất các mảng phần tử đơn lẻ và bắt đầu sử dụng hợp nhất từ bước 2, có vẻ như là thừa, bởi vì hợp nhất ban đầu cũng hoạt động tốt. Không có điểm nào trong việc tối ưu hóa điều đó. Nó chỉ giới thiệu các khái niệm và logic dư thừa.

— luk32

@ratchetfreak: Tôi cũng thích nó, nhưng thật đáng buồn là nó không tương đương với từ trên xuống (ít nhất là phiên bản tôi biết). Nó sẽ thực hiện việc hợp nhất một cách khác nhau, về cơ bản làm tròn đến độ dài mảng 2 sức mạnh tiếp theo, mà tôi nghĩ thậm chí có thể chậm hơn một chút. Bạn có biết một phiên bản từ dưới lên thực hiện chính xác việc sáp nhập mà không phải trả một khoản chi phí khổng lồ ở nơi nào khác không?

— dùng541686

@Mehrdad vấn đề thực sự duy nhất là cái đuôi nhỏ cần được hợp nhất. Trong trường hợp xấu nhất có nghĩa là một đường chuyền khác để hợp nhất trong một mục duy nhất cho các mảng có độ dài 1<<n+1. Mặc dù tôi chắc chắn rằng bạn có thể điều chỉnh mọi thứ để một cái đuôi quá nhỏ được hợp nhất ở đường chuyền thấp hơn.

— quái vật ratchet

@psmears "bạn không cần bất kỳ công việc nào từ máy tính để làm như vậy" - vì vậy tôi đoán chi phí hiệu năng của n cuộc gọi của một số hàm phân chia đệ quy (7 cuộc gọi trong sơ đồ ví dụ) về cơ bản là không đáng kể?

— Jimmy_Rustle

Tôi đoán những gì bạn có nghĩa là thực hiện từ dưới lên . Trong triển khai từ dưới lên, bạn bắt đầu từ các phần tử ô đơn lẻ di chuyển lên trên bằng cách hợp nhất các phần tử vào các danh sách / mảng được sắp xếp lớn hơn. Chỉ cần đảo ngược các mũi tên trong hình của bạn ở trên bắt đầu từ mảng giữa, tức là mảng một phần tử.

Ngoài ra, bạn có thể muốn tối ưu hóa sắp xếp hợp nhất bằng cách chia các mảng cho đến khi chúng đạt đến một kích thước không đổi, sau đó bạn chỉ cần sắp xếp chúng bằng cách sử dụng sắp xếp chèn ví dụ.

Mặt khác, sắp xếp mà không tách mảng là không thể. Trong thực tế, ý chính của sắp xếp Hợp nhất là phân chia và sắp xếp các phân đoạn, nghĩa là phân chia và chinh phục.

— fade2black
nguồn