Có thể bản thân thuật toán không tối nghĩa, nhưng ai có thể đặt tên cho một triển khai thực sự được sử dụng trong thực tế? Tôi có thể!
TIGCC (trình biên dịch dựa trên GCC cho máy tính vẽ đồ thị TI-89/92 / V200) sử dụng sắp xếp Shell để qsortthực hiện trong thư viện chuẩn của nó:
__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
unsigned short gap,byte_gap,i,j;
char *p,*a,*b,temp;
for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1) // Yes, this is not a quicksort,
{ // but works fast enough...
byte_gap=gap*(unsigned short)size;
for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
{
a=p; b=p+byte_gap;
if(cmp_func(a,b)<=0) break;
for(j=size;j;j--)
temp=*a, *a++=*b, *b++=temp;
}
}
}
Shell sort đã được chọn để ủng hộ quicksort để giữ kích thước mã thấp. Mặc dù độ phức tạp không triệu chứng của nó kém hơn, TI-89 không có nhiều RAM (190K, trừ kích thước chương trình và tổng kích thước của bất kỳ biến không lưu trữ nào), do đó có thể an toàn khi cho rằng số lượng vật phẩm sẽ phía dưới.
Một triển khai nhanh hơn đã được viết sau khi tôi phàn nàn về việc nó quá chậm trong một chương trình tôi đang viết. Nó sử dụng kích thước khoảng cách tốt hơn, cùng với tối ưu hóa lắp ráp. Nó có thể được tìm thấy ở đây: qsort.c
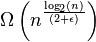 cho ε > 0.
cho ε > 0.