Tại sao không thể mô tả lượng tử được mô tả bằng mô hình cổng?

Đây là một câu hỏi tôi được truyền cảm hứng để hỏi dựa trên câu hỏi này , trong đó lưu ý rằng ủ lượng tử là một mô hình hoàn toàn khác để tính toán so với mô hình mạch thông thường. Tôi đã nghe điều này trước đây và tôi hiểu rằng mô hình cổng không áp dụng cho ủ lượng tử, nhưng tôi chưa bao giờ hiểu tại sao, hoặc làm thế nào để phân tích các tính toán mà một người thông báo có thể làm. Theo tôi hiểu từ một số cuộc nói chuyện (một số do chính D-wave!) Thực tế là những người ủ tóc bị giới hạn trong một Hamiltonian cụ thể chơi trong đó.

Một Annealer Quantum, chẳng hạn như một máy D-Wave là một đại diện vật lý của mô hình Ising và như vậy có 'vấn đề' Hamiltonian của mẫu

Về cơ bản, vấn đề cần giải quyết được ánh xạ tới Hamiltonian ở trên. Hệ thống bắt đầu với Hamilton và tham số ủ, s được sử dụng để lập bản đồ ban đầu Hamilton H Tôi cho vấn đề Hamilton H P sử dụng H ( s ) = ( 1 - s ) H I + s H P .$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

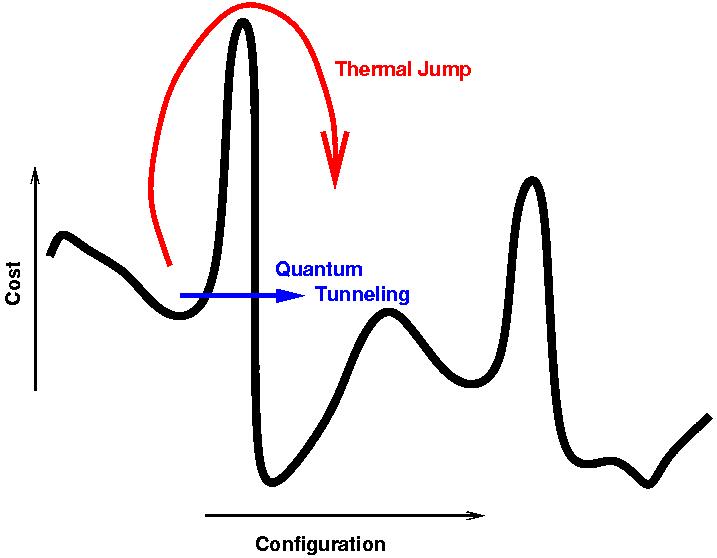
Vì đây là một anneal, quá trình này được thực hiện đủ chậm để ở gần trạng thái cơ bản của hệ thống trong khi Hamiltonian khác với vấn đề, sử dụng đường hầm để ở gần trạng thái cơ bản như được mô tả trong câu trả lời của Nat .

Bây giờ, tại sao điều này không thể được sử dụng để mô tả một mô hình cổng QC? Trên đây là vấn đề tối ưu hóa nhị phân không giới hạn Quadratic (QUBO) , đó là NP-hard ... Thật vậy, đây là một bài viết ánh xạ một số vấn đề NP cho mô hình Ising . Bất kỳ vấn đề nào trong NP đều có thể được ánh xạ tới bất kỳ vấn đề NP-hard nào trong thời gian đa thức và hệ số nguyên thực sự là một vấn đề NP.

Chà, nhiệt độ là khác không, vì vậy nó sẽ không ở trạng thái cơ bản trong suốt quá trình ủ và kết quả là, giải pháp vẫn chỉ là gần đúng. Hoặc, theo các cách khác nhau, xác suất thất bại lớn hơn một nửa (không nơi nào có xác suất thành công cao so với những gì một QC phổ quát coi là 'đàng hoàng' - đánh giá từ các biểu đồ tôi đã thấy, xác suất thành công cho máy hiện tại là khoảng và điều này sẽ chỉ trở nên tồi tệ hơn khi tăng kích thước) và thuật toán anneal không bị giới hạn lỗi. Ở tất cả. Như vậy, không có cách nào để biết liệu bạn có giải pháp chính xác với thứ gì đó như hệ số nguyên hay không.$0.2\%$

Những gì nó (về nguyên tắc) làm rất gần với kết quả chính xác, rất nhanh, nhưng điều này không giúp ích gì cho bất cứ điều gì mà kết quả chính xác được yêu cầu như chuyển từ 'gần đúng' sang 'chính xác' vẫn là một điều cực kỳ khó khăn ( tức là có lẽ vẫn còn NP nói chung, khi vấn đề ban đầu là vấn đề NP) trong trường hợp này, vì các tham số là / đưa ra giải pháp 'gần đúng' không nhất thiết phải được phân phối ở bất kỳ đâu gần các tham số được đưa ra giải pháp đúng.

Chỉnh sửa để làm rõ: điều này có nghĩa là một annealer lượng tử (QA) vẫn cần thời gian theo cấp số nhân (mặc dù có khả năng là thời gian theo cấp số nhân nhanh hơn) để giải quyết các vấn đề NP như hệ số nguyên, trong đó QC phổ biến tăng tốc theo cấp số nhân và có thể giải quyết tương tự vấn đề trong thời gian poly. Đây là những gì ngụ ý rằng QA không thể mô phỏng QC phổ quát trong thời gian poly (nếu không nó có thể giải quyết các vấn đề trong thời gian poly mà nó không thể). Như đã chỉ ra trong các bình luận, điều này không giống như nói rằng QA không thể tăng tốc tương tự trong các vấn đề khác, chẳng hạn như tìm kiếm cơ sở dữ liệu.

Ủng hộ nhiều hơn một chiến thuật tương tự.

Ý chính là bạn có một số chức năng kỳ lạ mà bạn muốn tối ưu hóa. Vì vậy, bạn nảy xung quanh nó. Lúc đầu, " nhiệt độ " rất cao, sao cho điểm được chọn có thể nảy ra xung quanh rất nhiều. Sau đó, khi thuật toán " nguội đi ", nhiệt độ giảm xuống và độ nảy trở nên ít tích cực hơn.

Cuối cùng, nó lắng xuống một tối ưu cục bộ, lý tưởng nhất là thuận lợi như tối ưu toàn cầu.

Đây là một hình ảnh động để ủ mô phỏng (không lượng tử):

Nhưng, đó là khá nhiều khái niệm tương tự cho ủ lượng tử :

Ngược lại, cổng logic là kỹ thuật số hơn nhiều so với analog. Nó liên quan đến các qubit và các hoạt động logic hơn là chỉ tìm thấy một kết quả sau khi nảy hỗn loạn.