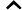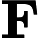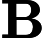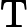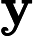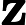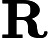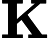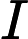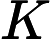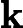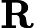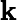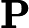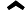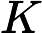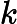Làm thế nào để hiểu Kalman đạt được bằng trực giác?

Các thuật toán Kalman filter hoạt động như sau

Khởi tạo và .$\hat{\textbf{x}}_{0|0}$$\textbf{P}_{0|0}$

Ở mỗi lần lặp$k=1,\dots,n$

Dự đoán

Dự đoán trạng thái (tiên nghiệm) dự đoán Dự đoán (a prori) ước tính hiệp phương sai Cập nhật

$$\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k} \textbf{u}_{k}$$ $$\textbf{P}_{k|k-1} = \textbf{F}_{k} \textbf{P}_{k-1|k-1} \textbf{F}_{k}^{\text{T}} + \textbf{Q}_{k}$$

Đổi mới hoặc đo lường dư Đổi mới (hoặc dư) hiệp phương sai tối ưu Kalman tăng Cập nhật (một posteriori) ước tính tình trạng Đã cập nhật (a posteriori) ước tính hiệp phương sai

$$\tilde{\textbf{y}}_k = \textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1}$$ $$\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k$$ $$\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}$$ $$\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k$$ $$\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}$$

Độ lợi Kalman biểu thị tầm quan trọng tương đối của lỗi đối với ước tính trước .$K_k$$\tilde{\textbf{y}}_k$$\hat{\textbf{x}}_{k|k-1}$

Tôi tự hỏi làm thế nào để hiểu công thức cho Kalman đạt được trực giác ? Hãy xem xét trường hợp khi các trạng thái và đầu ra là vô hướng, tại sao mức tăng lớn hơn, khi$K_k$

• $\textbf{P}_{k|k-1}$ lớn hơn

• $\textbf{H}_k$ lớn hơn

• $\textbf{S}_k$ nhỏ hơn?

Cảm ơn và trân trọng!

Tôi tìm thấy một cách tốt để suy nghĩ bằng trực giác của Kalman Gain . Nếu bạn viết theo cách này$K$$K$

$\displaystyle \quad\ \bf{K_k} = \bf{P_k^-\, H_k^{\rm T} (H_k P_k^-\, H_k^{\rm T} + R_k)^{-1}} = \bf{\frac {P_k^-\, H_k^{\rm T}}{H_k P_k^-\, H_k^{\rm T} + R_k}}$

bạn sẽ nhận ra rằng cường độ tương đối của ma trận ( ) và ( ) kiểm soát mối quan hệ giữa việc sử dụng ước tính trạng thái dự đoán ( ) và phép đo ( ) của bộ lọc .$R_k$$P_k$$x_{k}⁻$$ỹ_k$

$\displaystyle \quad\ \lim\limits_{\bf{R_k \to 0}} \bf{{P_k^-\, H_k^{\rm T}} \over\ {H_k P_k^-\, H_k^{\rm T} + R_k}}\ = \bf{H_k^{-1}}$

$\displaystyle \quad\ \lim\limits_{\bf{P_k \to 0}} \bf{{P_k^-\, H_k^{\rm T}} \over\ {H_k P_k^-\, H_k^{\rm T} + R_k}}\ = \bf 0$

Thay thế giới hạn đầu tiên vào phương trình cập nhật đo lường

$\displaystyle \quad\ \bf{\hat x_k} = \bf{x_k^-} + \bf{K_k}(\bf{\tilde y_k}-\bf{H_k}\bf{x_k^-})$

gợi ý rằng khi độ lớn của nhỏ, có nghĩa là các phép đo là chính xác, ước tính trạng thái phụ thuộc chủ yếu vào các phép đo.$R$

Khi trạng thái được biết chính xác, thì nhỏ so với và bộ lọc chủ yếu bỏ qua các phép đo thay vào dự đoán xuất phát từ trạng thái trước đó ( ).$H P^⁻ H^T$$R$$x_k⁻$

Độ lợi Kalman cho bạn biết tôi muốn thay đổi ước tính của mình bao nhiêu bằng cách đo.

${\bf S}_k$ là ma trận hiệp phương sai ước tính của các phép đo . Điều này cho chúng tôi biết "sự thay đổi" trong các phép đo của chúng tôi. Nếu nó lớn, điều đó có nghĩa là các phép đo "thay đổi" rất nhiều. Vì vậy, sự tự tin của bạn trong các phép đo này là thấp. Mặt khác, nếu nhỏ , độ biến thiên thấp, độ tin cậy của chúng tôi trong phép đo tăng lên. Khi chúng tôi tự tin về các phép đo của mình, đã tự tin rằng thông tin chúng tôi có được là đủ tốt để chúng tôi cập nhật / thay đổi các ước tính trạng thái của mình. Vì vậy, mức tăng Kalman cao hơn.${\bf z}_k$${\bf S}_k$

${\bf P}_k$ là ma trận hiệp phương sai trạng thái ước tính. Điều này cho chúng ta biết "tính biến đổi" của trạng thái, . Nếu lớn , điều đó có nghĩa là trạng thái được ước tính sẽ thay đổi rất nhiều. Vì vậy, bạn cần có thể thay đổi ước tính của mình với các phép đo mới. Kết quả là, mức tăng Kalman cao hơn.${\bf x}_k$${\bf P}_k$

Ngược lại, nếu nhỏ, thì bạn biết rằng trạng thái của bạn không thay đổi nhiều, vì vậy bạn không muốn thay đổi ước tính của mình quá nhiều mỗi lần. Câu trả lời của @ Jav_Rock nói rằng nếu , thì . Nói cách khác, anh ta ngụ ý rằng nếu bạn nghĩ rằng trạng thái của bạn không còn thay đổi nữa, bạn không cố gắng thay đổi ước tính của mình nữa.${\bf P}_k$${\bf P}_k \rightarrow 0$$K\rightarrow 0$

Jav_Rock có điểm. Trên thực tế nếu bạn viết như thế này$\bf{K_k}$

$\displaystyle \quad\ \bf{K_k} = \bf{P_k^-\, H_k^{\rm T} (H_k P_k^-\, H_k^{\rm T} + R_k)^{-1}} = \bf{H_k^-\frac {H_kP_k^-\, H_k^{\rm T}}{H_k P_k^-\, H_k^{\rm T} + R_k}}$

tử số của phân số là viết tắt của độ không đảm bảo được truyền từ mô hình trong khi là viết tắt của độ không đảm bảo từ phép đo. Vì vậy, giá trị của phân số là số lượng chúng ta nên tin tưởng vào phép đo, như được giải thích bởi Jav_Rock.$\bf{R_k}$

Đối với , nó chỉ chuyển đổi quan sát trở lại trạng thái, bởi vì đó là trạng thái mà chúng tôi muốn cập nhật, không phải là quan sát.$\bf{H_k^-}$

Để kết thúc, hệ số tính toán mức độ hiệu chỉnh mà chúng ta nên thực hiện từ quan sát và chuyển đổi hiệu chỉnh quan sát trở lại hiệu chỉnh trạng thái, dẫn đến cập nhật ước tính trạng thái:$\bf{K_k}$

$\displaystyle \quad\ \bf{\hat x_k} = \bf{x_k^-} + \bf{K_k}(\bf{\tilde y_k}-\bf{H_k}\bf{x_k^-})$

Tôi đang làm việc trên thuật toán Kalman Filter (KF). Tôi quan sát thấy rằng kalman đạt được thỏa thuận với sự hội tụ của thuật toán với thời gian, nghĩa là thuật toán sửa chữa nhanh như thế nào và giảm thiểu phần dư.

Đến với phương trình, chọn một giá trị tăng kalman ban đầu và thay đổi nó từ thấp đến cao, có thể cung cấp cho bạn một giá trị gần đúng.