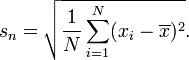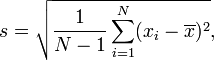Tại sao các trường Hoa Kỳ và Vương quốc Anh dạy các phương pháp khác nhau để tính độ lệch chuẩn?

15

Theo tôi hiểu, các trường ở Anh dạy rằng Độ lệch chuẩn được tìm thấy bằng cách sử dụng:

$alt text$

trong khi các trường Hoa Kỳ dạy:

$alt text$

(ở mức cơ bản nào).

Điều này đã gây ra một số vấn đề sinh viên của tôi trong quá khứ khi họ đã tìm kiếm trên Internet, nhưng tìm thấy lời giải thích sai.

Tại sao lại có sự khác biệt?

Với các bộ dữ liệu đơn giản cho biết 10 giá trị, mức độ lỗi sẽ xảy ra nếu áp dụng phương pháp sai (ví dụ: trong một bài kiểm tra)?

— A-mốt
nguồn

4

Tôi không chắc liệu đặc trưng của cái này hay cái kia là công thức 'sai' là cách để hiểu vấn đề. Nó chỉ là cái thứ hai là 'tốt hơn' theo nghĩa nó là một công cụ ước tính không thiên vị về độ lệch chuẩn thực sự. Vì vậy, nếu bạn quan tâm đến các ước tính không thiên vị thì cái thứ hai là 'tốt hơn' / 'chính xác'.

Tôi đã mô tả công thức là "sai" hoàn toàn theo nghĩa là trong một bài kiểm tra nếu bạn sử dụng công thức không được quy định bởi giáo trình, bạn sẽ kết thúc bằng câu trả lời "sai". Ngoài ra, nếu các giá trị không phải là một mẫu dân số mỗi se thì chắc chắn công thức đầu tiên cho giá trị chính xác hơn.

— A-mốt

13

Srikant, tôi không nghĩ rằng cái thứ hai là một công cụ ước tính không thiên vị. Bình phương của nó là một ước lượng không thiên vị của phương sai thực sự. Tuy nhiên, bất đẳng thức của Jensen xác định rằng kỳ vọng của hàm độ cong của một biến ngẫu nhiên không giống như hàm kỳ vọng của biến ngẫu nhiên. Do đó, công thức thứ hai không thể là một công cụ ước lượng không thiên vị về độ lệch chuẩn thực.

— Andrew Robinson

Để tham khảo chéo: nó cũng được hỏi @ m.SE ...

— JM không phải là một nhà thống kê

2

Bất kỳ trường Mỹ bằng cách sử dụng văn bản tiểu rất phổ biến bởi Freedman, Pisani, & Purves đang sử dụng công thức đầu tiên (

), vì vậy nó có vẻ không chính xác để mô tả điều này như một Mỹ vs Anh khác biệt.

s_{n}

$s_n$

— whuber

18

Công thức đầu tiên là độ lệch chuẩn dân số và công thức thứ hai là độ lệch chuẩn mẫu . Công thức thứ hai cũng liên quan đến công cụ ước lượng không thiên vị của phương sai - xem wikipedia để biết thêm chi tiết.

Tôi cho rằng (ở đây) ở Anh, họ không phân biệt giữa mẫu và dân số ở trường trung học. Họ chắc chắn không chạm vào các khái niệm như công cụ ước tính thiên vị.

— csgillespie
nguồn

4

Colin, một công cụ ước tính không thiên vị về độ lệch chuẩn không có biểu diễn dạng đóng trong trường hợp chung. Cái tồn tại là công cụ ước tính không thiên vị của phương sai (s 2 trong trường hợp này). Đáng chú ý là cả hai đều là các công cụ ước tính nhất quán của phương sai dân số - và do đó theo định lý ánh xạ liên tục, là hai công cụ ước tính của độ lệch chuẩn. Một điểm liên quan là s n 2 có MSE thấp hơn s 2 . Lợi thế bổ sung từ việc áp đặt không thiên vị là có thể tranh cãi.

— mornington

@Tirthankar - Rất cẩu thả của tôi. Tôi đã thay đổi câu trả lời một chút. Cảm ơn.

— csgillespie

2

Theo như tôi nhớ, tôi đã được dạy về phép tính 'mẫu' trong toán học và khoa học của GCSE (tuổi 14-16) và sự khác biệt giữa dân số và mẫu và các biện pháp phương sai liên quan của họ được đề cập (mặc dù không sâu) ở cấp độ A ( tuổi 16-18). Vì vậy, tôi không chắc đây là một sự khác biệt đơn giản giữa Anh / Mỹ.

— Freya Harrison

11

Bởi vì chưa ai trả lời câu hỏi cuối cùng - cụ thể là, để định lượng sự khác biệt giữa hai công thức - chúng ta hãy quan tâm đến điều đó.

Vì nhiều lý do, nên so sánh độ lệch chuẩn về tỷ lệ thay vì sự khác biệt của chúng. Tỷ lệ là

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

Phép tính gần đúng có thể được xem là cắt ngắn chuỗi Taylor (xen kẽ) cho căn bậc hai, cho biết lỗi không thể vượt quá =. Điều này chứng tỏ rằng xấp xỉ là quá đủ tốt (cho mục đích của chúng tôi) một khilàhoặc lớn hơn. $|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ đánh giá hoặc dự đoán (chẳng hạn như sử dụng 68-95 -99,7 quy tắc của ngón tay cái). Sự khác biệt thậm chí còn ít quan trọng hơn khi so sánhSD, chẳng hạn như khi so sánh sự lây lan của hai bộ dữ liệu. . đó có thể được coi là một dấu hiệu cho thấy văn bản hoặc lớp không thể nhấn mạnh những gì thực sự quan trọng.

$N$ $t$ $z$ $s$ $s_n$

— whuber
nguồn

6

Đây là sự điều chỉnh của Bessel . Phiên bản tại Hoa Kỳ đang hiển thị công thức cho độ lệch chuẩn mẫu , trong đó phiên bản Vương quốc Anh ở trên là độ lệch chuẩn của mẫu .

— Sậy Copsey
nguồn

5

Tôi không chắc đây hoàn toàn là vấn đề của Mỹ so với Anh. Đây là một trang ngắn gọn mà tôi đã viết giải thích sự khác biệt giữa việc sử dụng n so với n-1 khi tính toán Độ lệch chuẩn .

— Harvey Motulsky
nguồn

1

Tôi không gợi ý rằng, tôi chỉ tò mò về lý do tại sao một sự khác biệt như vậy có thể phát sinh, mức độ lỗi nào theo lời khuyên sai có thể đưa ra và liệu có một lời giải thích đúng đắn về sự khác biệt mà tôi có thể đưa ra cho các học sinh của mình .

— A-mốt

3

Vì N là số điểm trong tập dữ liệu, nên người ta có thể lập luận rằng bằng cách tính giá trị trung bình, người ta đã giảm mức độ tự do trong tập dữ liệu (do người ta đưa phụ thuộc vào tập dữ liệu), vì vậy người ta nên sử dụng N -1 khi ước tính độ lệch chuẩn từ một tập dữ liệu mà người ta phải ước tính giá trị trung bình trước đó.

— Benjamin Bannier
nguồn