Hình dạng giống như cái nêm của âm mưu PCA chỉ ra điều gì?

Trong bài báo của họ về bộ tự động để phân loại văn bản, Hinton và Salakhutdinov đã trình bày cốt truyện được tạo ra bởi LSA 2 chiều (có liên quan chặt chẽ với PCA) : .

Áp dụng PCA cho dữ liệu chiều cao hoàn toàn khác nhau, tôi đã có được một âm mưu tương tự: (ngoại trừ trong trường hợp này tôi thực sự muốn biết liệu có cấu trúc bên trong nào không).

Nếu chúng ta cung cấp dữ liệu ngẫu nhiên vào PCA, chúng ta sẽ có được một đốm hình đĩa, vì vậy hình dạng hình nêm này không phải là ngẫu nhiên. Nó có ý nghĩa gì không?

Giả sử các biến là dương hoặc không âm, các cạnh của cạnh chỉ là các điểm vượt quá dữ liệu sẽ trở thành 0 hoặc âm tương ứng. Vì dữ liệu thực tế như vậy có xu hướng bị lệch, chúng ta thấy mật độ điểm lớn hơn ở đầu phân phối thấp và do đó mật độ lớn hơn tại "điểm" của nêm.

Tổng quát hơn, PCA chỉ đơn giản là một vòng quay của dữ liệu và các ràng buộc trên các dữ liệu đó thường sẽ hiển thị trong các thành phần chính theo cách tương tự như trong câu hỏi.

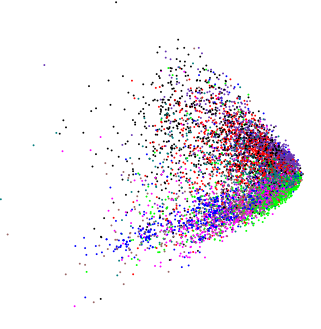
Dưới đây là một ví dụ sử dụng một số biến phân phối thông thường log:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

Tùy thuộc vào vòng quay được ngụ ý bởi hai PC đầu tiên, bạn có thể thấy cái nêm hoặc bạn có thể thấy một phiên bản hơi khác, hiển thị ở đây dưới dạng 3d bằng cách sử dụng ( ordirgl()thay cho plot())

Ở đây, trong 3d chúng ta thấy nhiều gai nhô ra từ khối trung tâm.

$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

Và đối với các biến ngẫu nhiên dương đồng nhất, chúng ta thấy một khối

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Lưu ý rằng ở đây, để minh họa, tôi hiển thị đồng phục chỉ bằng 3 biến ngẫu nhiên do đó các điểm mô tả một khối lập phương trong 3d. Với kích thước cao hơn / nhiều biến hơn, chúng ta không thể biểu thị hypercube 5d một cách hoàn hảo trong 3d và do đó hình dạng "khối" riêng biệt bị biến dạng phần nào. Các vấn đề tương tự ảnh hưởng đến các ví dụ khác được hiển thị, nhưng vẫn dễ dàng nhận thấy các ràng buộc trong các ví dụ đó.

Đối với dữ liệu của bạn, một phép biến đổi nhật ký của các biến trước PCA sẽ kéo theo các đuôi và kéo dài dữ liệu bị vón cục, giống như bạn có thể sử dụng phép biến đổi như vậy trong hồi quy tuyến tính.

Các hình dạng khác có thể mọc lên trong các ô PCA; một hình dạng như vậy là một vật phẩm của đại diện số liệu được bảo tồn trong PCA và được gọi là móng ngựa . Đối với dữ liệu có độ dốc dài hoặc chiếm ưu thế (các mẫu được sắp xếp theo một chiều duy nhất với các biến tăng từ 0 đến tối đa và sau đó giảm xuống 0 dọc theo các phần của dữ liệu được biết là tạo ra các vật phẩm như vậy.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

tạo ra một móng ngựa cực đoan, trong đó các điểm ở hai đầu của trục uốn cong vào giữa.