Định lý Bayes là gì?

Các ý chính, nghĩa là các khái niệm liên quan đến định lý Bayes là gì? Tôi không yêu cầu bất kỳ dẫn xuất của ký hiệu toán học phức tạp.

Định lý Bayes là một kết quả tương đối đơn giản, nhưng cơ bản của lý thuyết xác suất cho phép tính toán các xác suất có điều kiện nhất định. Xác suất có điều kiện chỉ là những xác suất phản ánh ảnh hưởng của một sự kiện đến xác suất của sự kiện khác.

Nói một cách đơn giản, ở dạng nổi tiếng nhất, nó nói rằng xác suất của một giả thuyết được cung cấp dữ liệu mới ( P (H | D) ; được gọi là xác suất sau) bằng với phương trình sau: xác suất của dữ liệu được quan sát đưa ra giả thuyết ( P (D | H) ; được gọi là xác suất có điều kiện), nhân với xác suất của lý thuyết là đúng trước bằng chứng mới ( P (H) ; được gọi là xác suất trước của H), chia cho xác suất nhìn thấy dữ liệu đó, khoảng thời gian ( P (D ); được gọi là xác suất cận biên của D).

Chính thức, phương trình trông như thế này:

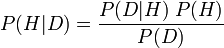
Tầm quan trọng của định lý Bayes phần lớn là do cách sử dụng hợp lý của nó là một điểm bất đồng giữa các trường phái tư tưởng về xác suất. Đối với một Bayes chủ quan (diễn giải xác suất là mức độ tin tưởng chủ quan) Định lý của Bayes cung cấp nền tảng cho kiểm tra lý thuyết, lựa chọn lý thuyết và thực tiễn khác, bằng cách đưa các phán đoán xác suất chủ quan của họ vào phương trình và chạy theo nó. Đối với một người thường xuyên (diễn giải xác suất là giới hạn tần số tương đối ), việc sử dụng định lý Bayes này là một sự lạm dụng và thay vào đó họ cố gắng sử dụng các linh mục có ý nghĩa (không chủ quan) (như Bayesian khách quan theo cách giải thích xác suất khác).

Tôi xin lỗi, nhưng dường như có một số nhầm lẫn ở đây: Định lý của Bayes không được đưa ra để thảo luận về cuộc tranh luận không thường xuyên về Bayesian- Thường xuyên . Đó là một định lý phù hợp với cả hai trường phái tư tưởng (cho rằng nó phù hợp với các tiên đề xác suất của Kolmogorov).

Tất nhiên, định lý của Bayes là cốt lõi của thống kê Bayes, nhưng bản thân định lý này là phổ quát. Cuộc đụng độ giữa những người thường xuyên và Bayes chủ yếu liên quan đến cách phân phối trước có thể được xác định hay không.

Vì vậy, nếu câu hỏi là về định lý của Bayes (chứ không phải số liệu thống kê của Bayes):

Định lý Bayes định nghĩa cách người ta có thể tính xác suất có điều kiện cụ thể. Ví dụ, hãy tưởng tượng rằng bạn biết: xác suất ai đó có triệu chứng A, cho rằng họ mắc bệnh X p (A | X); xác suất có người nói chung mắc bệnh X p (X); xác suất ai đó nói chung có triệu chứng A p (A). với 3 thông tin này, bạn có thể tính xác suất ai đó mắc bệnh X, cho rằng họ có triệu chứng A p (X | A).

Định lý Bayes là một cách để xoay xác suất có điều kiện sang xác suất có điều kiện khác P ( B | A ) .$P(A|B)$$P(B|A)$

Một vấp ngã đối với một số người là ý nghĩa của . Đây là một cách để giảm không gian của các sự kiện có thể bằng cách chỉ xem xét những sự kiện mà A chắc chắn xảy ra (hoặc là đúng). Vì vậy, ví dụ xác suất rằng một con xúc xắc ném, công bằng, hiển thị sáu, P ( súc sắc sáu ) , là 1/6, tuy nhiên xác suất một con xúc xắc hạ cánh sáu cho rằng nó hạ cánh một số chẵn, P ( xúc xắc hạ cánh sáu | đất súc sắc chẵn ) , là 1/3.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

Bạn có thể tự rút ra định lý Bayes như sau. Bắt đầu với định nghĩa tỷ lệ của xác suất có điều kiện:

$P(B|A) = \frac{P(AB)}{P(A)}$

nơi là xác suất chung của A và B và P ( A ) là xác suất biên của Một .$P(AB)$$A$$B$$P(A)$$A$

Hiện tại công thức không tham chiếu đến , vì vậy hãy viết ra định nghĩa về điều này:$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

Một mẹo nhỏ để thực hiện công việc này là thấy (vì đại số Boolean nằm bên dưới tất cả những điều này, bạn có thể dễ dàng chứng minh điều này bằng bảng chân lý bằng cách hiển thị A B = B A ), để chúng ta có thể viết:$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

và hey thế là:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

Đối với vấn đề quan trọng là làm thế nào để xoay một xác suất có điều kiện theo cách này, hãy xem xét ví dụ phổ biến về việc cố gắng suy ra xác suất một người mắc bệnh cho rằng họ có triệu chứng, nghĩa là chúng ta biết rằng họ có triệu chứng - chúng ta có thể nhìn thấy nó - nhưng chúng ta không thể chắc chắn liệu họ có bị bệnh hay không và phải suy ra. Tôi sẽ bắt đầu với công thức và làm việc trở lại.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

Vì vậy, để giải quyết nó, bạn cần biết xác suất trước của triệu chứng, xác suất trước của bệnh (nghĩa là mức độ phổ biến hay hiếm gặp của triệu chứng và bệnh) và cũng có khả năng ai đó có triệu chứng mà chúng ta biết là ai đó mắc phải một căn bệnh (ví dụ, thông qua các xét nghiệm trong phòng thí nghiệm tốn kém thời gian).

Nó có thể trở nên phức tạp hơn nhiều so với điều này, ví dụ, nếu bạn có nhiều bệnh và triệu chứng, nhưng ý tưởng là như nhau. Thậm chí, nói chung, định lý của Bayes thường xuất hiện nếu bạn có lý thuyết xác suất về mối quan hệ giữa nguyên nhân (ví dụ: bệnh) và ảnh hưởng (ví dụ: triệu chứng) và bạn cần suy luận ngược (ví dụ: bạn thấy một số triệu chứng mà bạn muốn để suy ra căn bệnh tiềm ẩn).

Có hai trường phái tư tưởng chính là Thống kê: người thường xuyên và người Bayes .

Định lý Bayes là để làm với cái sau và có thể được coi là một cách để hiểu làm thế nào xác suất một lý thuyết là đúng bị ảnh hưởng bởi một bằng chứng mới. Điều này được gọi là xác suất có điều kiện. Bạn có thể muốn xem xét điều này để nắm được bài toán.

Hãy để tôi cung cấp cho bạn một cái nhìn sâu sắc rất trực giác. Giả sử bạn đang tung đồng xu 10 lần và bạn nhận được 8 đầu và 2 đuôi. Câu hỏi sẽ xuất hiện trong đầu bạn là liệu đồng tiền này có thiên về đầu hay không.

Bây giờ nếu bạn đi theo định nghĩa thông thường hoặc cách tiếp cận xác suất thường xuyên, bạn có thể nói rằng đồng tiền này không thiên vị và đây là một sự xuất hiện đặc biệt. Do đó, bạn sẽ kết luận rằng khả năng có được một cú đánh đầu tiếp theo cũng là 50%.

Nhưng giả sử bạn là người Bayes. Bạn thực sự sẽ nghĩ rằng vì bạn có số lượng đầu cực kỳ cao, nên đồng xu có xu hướng nghiêng về phía đầu. Có các phương pháp để tính toán sai lệch có thể này. Bạn sẽ tính toán chúng và sau đó khi bạn tung đồng xu vào lần tới, bạn chắc chắn sẽ gọi một người đứng đầu.

Vì vậy, xác suất Bayes là về niềm tin mà bạn phát triển dựa trên dữ liệu bạn quan sát. Tôi hy vọng điều đó là đủ đơn giản.

Định lý Bayes liên quan đến hai ý tưởng: xác suất và khả năng. Xác suất nói: đưa ra mô hình này, đây là những kết quả. Vì vậy: được trao một đồng tiền công bằng, tôi sẽ nhận được 50% thời gian. Likabilities nói: với những kết quả này, đây là những gì chúng ta có thể nói về mô hình. Vì vậy: nếu bạn tung đồng xu 100 lần và nhận 88 đầu (để lấy ví dụ trước và làm cho nó cực hơn), thì khả năng mô hình đồng xu công bằng là không quá cao.

Một trong những ví dụ tiêu chuẩn được sử dụng để minh họa cho định lý của Bayes là ý tưởng xét nghiệm bệnh: nếu bạn làm xét nghiệm chính xác 95% cho một bệnh mà 1 trong 10000 dân số mắc phải và bạn có kết quả dương tính thì khả năng nào là bạn có bị bệnh không?

Câu trả lời ngây thơ là 95%, nhưng điều này bỏ qua vấn đề rằng 5% bài kiểm tra trên 9999 trong số 10000 người sẽ cho kết quả dương tính giả. Vì vậy, tỷ lệ mắc bệnh của bạn thấp hơn 95%.

Việc tôi sử dụng cụm từ mơ hồ "cơ hội là gì" là có chủ ý. Để sử dụng ngôn ngữ xác suất / khả năng: xác suất xét nghiệm chính xác là 95%, nhưng điều bạn muốn biết là khả năng bạn mắc bệnh.

Hơi lạc đề: Một ví dụ kinh điển khác mà định lý Bayes được sử dụng để giải quyết trong tất cả các sách giáo khoa là vấn đề Monty Hall: Bạn đang tham gia một chương trình đố vui. Có một giải thưởng đằng sau một trong ba cánh cửa. Bạn chọn cửa một. Chủ nhà mở cửa ba để tiết lộ không có giải thưởng. Bạn có nên đổi sang cửa hai cơ hội?

Tôi thích cách viết lại câu hỏi (lịch sự của tài liệu tham khảo bên dưới): bạn đang tham gia một chương trình đố vui. Có một giải thưởng đằng sau một trong một triệu cánh cửa. Bạn chọn cửa một. Chủ nhà mở tất cả các cửa khác ngoại trừ cửa 104632 để tiết lộ không có giải thưởng. Có nên đổi sang cửa 104632?

Cuốn sách yêu thích của tôi bàn về định lý của Bayes, rất nhiều từ quan điểm của Bayes, là "Lý thuyết thông tin, suy luận và thuật toán học tập" của David JC MacKay. Đó là một cuốn sách báo của Đại học Cambridge, ISBN-13: YAM521642989. Câu trả lời của tôi là (tôi hy vọng) một sự chắt lọc các loại thảo luận được thực hiện trong cuốn sách. (Áp dụng quy tắc thông thường: Tôi không có liên kết với tác giả, tôi chỉ thích cuốn sách).

Định lý Bayes ở dạng rõ ràng nhất của nó chỉ đơn giản là một tuyên bố lại của hai điều:

1. the joint probability is symmetric in its arguments $P(HD|I)=P(DH|I)$
2. the product rule $P(HD|I)=P(H|I)P(D|HI)$

So by using the symmetry:

Now if $P(D|I) \neq 0$ you can divide both sides by $P(D|I)$ to get:

So this is it? How can something so simple be so awesome? As with most things "its the journey that's more important than the destination". Bayes theorem rocks because of the arguments that lead to it.

What is missing from this is that the product rule and sum rule $P(H|I)=1-P(\overline{H}|I)$, can be derived using deductive logic based on axioms of consistent reasoning.

Now the "rule" in deductive logic is that if you have a relationship "A implies B" then you also have "Not B implies Not A". So we have "consistent reasoning implies Bayes theorem". This means "Not Bayes theorem implies Not consistent reasoning". i.e. if your result isn't equivalent to a Bayesian result for some prior and likelihood then you are reasoning inconsistently.

This result is called Cox's theorem and was proved in "Algebra of Probable inference" in the 1940's. A more recent derivation is given in Proability theory: The logic of science.

I really like Kevin Murphy's intro the to Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

The quote here is from an economist article:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

The essence of the Bayesian approach is to provide a mathematical rule explaining how you should change your existing beliefs in the light of new evidence. In other words, it allows scientists to combine new data with their existing knowledge or expertise. The canonical example is to imagine that a precocious newborn observes his first sunset, and wonders whether the sun will rise again or not. He assigns equal prior probabilities to both possible outcomes, and represents this by placing one white and one black marble into a bag. The following day, when the sun rises, the child places another white marble in the bag. The probability that a marble plucked randomly from the bag will be white (ie, the child's degree of belief in future sunrises) has thus gone from a half to two-thirds. After sunrise the next day, the child adds another white marble, and the probability (and thus the degree of belief) goes from two-thirds to three-quarters. And so on. Gradually, the initial belief that the sun is just as likely as not to rise each morning is modified to become a near-certainty that the sun will always rise.